Informatické myšlení (3): příklady ze skutečnosti

Lizina lednička, jedna z mnoha

Dnešním příspěvkem se vracím k sérii o informatickém myšlení. Konečně se dostáváme od neurčitého povídání k nějakým příkladům. Nejasnosti tím nekončí, ale diskutovat se dá konkrétněji: Je ten který příklad opravdu ukázkou informatického myšlení? Proč ano, proč ne?
Skočíme do toho rovnýma nohama: informatické myšlení nikoliv ve výuce, ale v opravdovém životě (ve škole je přece život jenom jako).

 Triviální příklady

Už v prvním příspěvku jsem několik příkladů uvedl: balení školní brašny (prefetching), organizace jogurtů v lednici podle data spotřeby (prioritní fronta). Telefonní linka fungující i při výpadku proudu (redundance, nezávislost selhání). To jsou příklady tak jednoduché, že kvůli nim opravdu není třeba studovat informatiku.

Podobně jednoduchým příkladem je pipeline v jídelně. Nikoho snad ani nenapadne neseřadit „nějak rozumně“ výdej táců, příborů, polévky, jednoho z hlavních jídel, ovoce, sklenic a nápojů, aby strávníci mohli postupovat pěkně v řadě a nevráželi do sebe. Čas od času ovšem narazíme na situaci ekvivalentní, jenže mimo známý jídelnový kontext — a organizace se změní v chaos. Nebo jiný příklad: znáte někoho, kdo potřeboval změnit uspořádání zásuvek v komodě? A přehazoval jejich obsah, nebo prostě zaměnil celé zásuvky?

Tyto triviální příklady ukazují, že se informatické principy najdou i v doslova každodenním životě. Čím je situace jednodušší, tím spíše ji zdárně vyřešíme i bez znalosti informatiky. Podobně i hmotnost cihly z úlohy „cihla váží kilo a půl cihly" zjistíme bez znalosti rovnic. Vybíráte si k zaplacení nákupu opravdu nejvhodnější pokladnu, nebo jen tak odhadujete? A z pohledu obchodníka: naplníte regál intuitivně, nebo přijdete s robustnějším řešením? A co teprve organizace skladu?


Čím je situace složitější, tím víc informatika zvýší šance na úspěch.

Počítání párů

Poslední jednoduchý příklad rozeberu podrobněji:

Učitel tance na konci lekce vyzývá k přihlášení zvednutím ruky ty páry, kterým vyhovuje páteční termín závěrečného plesu, a spočte zvednuté ruce. Následně se ptá, komu vyhovuje termín sobotní. Ke zvednutí ruky ale již vyzývá jen dámy.

Učitel tance právě na okamžik zauvažoval jako informatik a uvědomil si, jak zkrátit čas počítání přibližně polovinu. Ihned se nabízí dvě námitky:

1. Není to matematika? Není. Matematicky jsou správně oba postupy, oba dávají správný výsledek. Při výuce matematiky se zkoumáním efektivity vyučovaných a používaných postupů zabýváme velmi zřídkakdy.
2. Učitel tance k tomuhle nemusí být informatik, stačí mu přece zdravý rozum. Ano. Tak jako v případě ostatních předmětů, i informatické problémy lze, pokud jsou jednoduché, správně vyřešit intuitivně. Odpověď leží v kvalitě života, které chceme dosahovat. Jistě lze šťastně žít i bez informatického myšlení. V principu podobně, jako lze šťastně žít bez dovednosti číst, psát a počítat, nebo si tepelně upravovat jídlo.

Složitější příklad: trumpetista

Trumpetista a informatik Roger Dannenberg si měl stejně jako ostatní členové kapely vybrat daných asi 40 skladeb pro daný večer z neseřazené složky asi dvou set. To je dost na to, aby se vyplatilo nejdřív zamyslet nad časovou efektivitou zvoleného postupu. Všichni ostatní začali postupně procházet složku a po jednom hledat a vybírat skladby. V takové situaci R. Dannenberg se rozhodl seřadit 200 skladeb v čase O(N·log(N)) (N je velikost složky, zde 200) a teprve potom najít hledané skladby, tedy už v čase O(M·log(N)), namísto O(M·N) (M je počet hledaných skladeb, tedy 40), tak jako ostatní. Sice pořád ještě řadil, zatímco ostatní byli zpola hotovi a podivovali se jeho počínání — skončil nicméně jako první.

Poznamenám, že v takové situaci nestačí použít heuristiku „vždycky je lepší je řadit“ nebo horní odhady složitosti. Pokud totiž nejsou vstupy přesvědčivě veliké nebo nemáme dostatečnou zkušenost, není ihned zřejmé, jestli řazení není zbytečná práce. Kdyby byl rozdíl v počtu skladeb k vyhledání M a počtu skladeb ve složce N výraznější, mohlo by být rychlejší přímo hledat.

Dále je nutno si uvědomit, že O(M·N) zde nelze ztotožnit s M·N, pravděpodobně bychom totiž náš odhad o 100% nadhodnotili. Trvání úkonů při řazení a při hledání není jednoduše zaměnitelné. Další otázkou je vhodná volba řadicího algoritmu pro dané podmínky (tedy řazení nikoliv čísel v paměti, ale papírů v lidských rukách). Pochopitelně platí, že čím větší problém je, tím častěji převáží (správně použitá) obecná informatická teorie nad konkrétními okolnostmi.

A nakonec si položme otázku, jestli by nebylo bývalo lepší celou úlohu obrátit naruby. Postupně projít složku a pro každou skladbu (kterou stejně vezmeme do ruky a přečteme její název) zkontrolovat, jestli se se nachází v předem seřazeném seznamu 40 vybraných skladeb. Celkově potřebujeme čas O(M·log(M)) na seřazení seznamu a O(N·log(M)) na vyhledání vybraných skladeb, tedy řešení v tomto případě ještě lepší. Navíc je toto řešení obecně lepší častěji, tedy ve více obdobných situacích.

Tyto úvahy měly ukázat, že k efektivnímu vyřešení problému nepostačí pouhé znalosti informatiky. Je nutno jako informatik přemýšlet, znalosti použít i v nových situacích. Zahrnutí tradičního obsahu vědní informatiky do výuky proto samo o sobě IM nutně nerozvíjí. Výpočet očekávané složitosti QuickSortu není rozhodující (byť je užitečný) v situaci, kdy je hlavním omezením efektivity fakt, že máme k dispozici pouze dvě ruce.

Ledviny a závěr

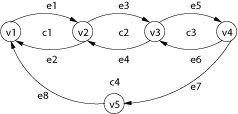Schéma možných řetězů příjemců a dárců ledvin
(Abraham, D., Blum, A., and Sandholm, T.)

Na závěr připomenu příklad s ledvinami popsaný také hned v prvním příspěvku o informatickém myšlení, je totiž můj nejoblíbenější. Zapojení informatiky do procesu hledání dárců ledvin zachraňuje lidské životy. Přitom nestačí být dobrý doktor, ani nestačí umět dobře používat počítač. Někdo musí porozumět podstatě problému dost do hloubky, a zároveň se na něj podívat z nového úhlu pohledu a zhodnotit, jestli by nešlo použít lepší postupy k řešení, než doposud. Nejde samozřejmě o to, aby každý dovedl vytvářet algoritmy na optimální řetězové transplantace. Každý by ale měl poznat, že to je úloha, kde se nejspíš dobře uplatní informatika.

Znáte další příklady informatického myšlení ze života? Uveďte je do diskuse! IM je dost nový pojem, a dost důležitý, pracuje s ním např. vládní strategie digitálního vzdělávání. Je nejvyšší čas si vyjasnit, co informatické myšlení je, a co není.

Tento příspěvek vychází z článku Lessner, Daniel: Analýza významu pojmu „Computational Thinking“. In: Journal of Technology and Information Education, 6 (1), Olomouc 2014, pp. 71—88.